Ces exercices sont issues de devoir en classe ou à la maison donnés dans les années 2000, 2001, 2002; certains demandent de la réflexion. Le plus simple est de les imprimer et de travailler tranquillement sur papier. Les corrigés suivront...

EXERCICE 1 : Dans le repère 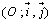orthonormé direct, on considère le point A(1 ; 0). Soit r la rotation de centre O et d'angle .
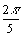a) Faire un dessin en prenant l'unité du repère = 4 cm. Construire les points B, C, D, E définis par r ( A) = B ; r (B) = C ; r (C) = D ; r (D) = E.
b) Quelle est l'image de E par r ?
c) Préciser la mesure principale des angles de vecteurs , , .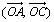
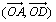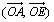d) Montrer que 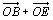et 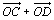sont colinéaires à .
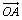e) Montrer que 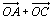et 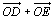sont colinéaires à .
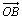f) En déduire que .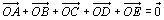
g) Déterminer les coordonnées des points B, C, D, E dans .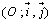
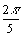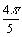h ) Déduire de la question e) qu'il existe un réel l tel que 1 + cos(4p5) = l cos() et sin() = l sin() .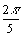
i ) En utilisant la propriété : pour tout réel x , on a cos²x + sin²x = 1, montrer que l = 2 cos().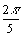
j ) Déduire de la question f) que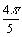 cos() + cos(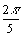) + 12 = 0.
k ) Montrer que le nombre cos(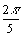) est solution de l'équation 2x ² + x - 12 = 0. En déduire les valeurs exactes de co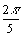s() et cos().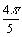

EXERCICE 2: On considère le repère orthonormé direct .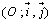
a) Placer les points C, D, E définis par leur coordonnées polaires C( 1 ; 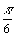) , D( 2 ; 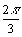) , E( 4 ; - ) .
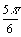b) Déterminer les coordonnées cartésiennes des points C, D, E .
c) Déterminer la mesure principale des angles orientés 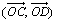et .
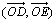d) En déduire la nature des triangles ODC et ODE.
e) On pose 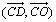= a ; montrer que 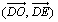= - a .
f) En déduire la nature du triangle CDE.
g) Calculer les longueurs CD, CE et DE et retrouver le résultat de la question précédente.

EXERCICE 3: On considère le triangle ACD équilatéral, et les triangles ABC et DEA rectangles et isocèles respectivement en B et E ( extérieur à ACD ) .
a) Déterminer la mesure des angles géométriques ^BAE et ^BCD .
b) En déduire une mesure, en radians, des angles orientés 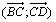et .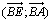
c) En utilisant la relation de Chasles, déterminer une mesure, en radians, de l'angle orienté .
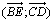d) Que peut-on en déduire pour les droites (BE) et (CD) ?

EXERCICE 4: On considère le repère orthonormé direct .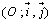
a) Placer les points C, D, E définis par leur coordonnées polaires C( 2 ; 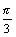) , D( 1 ; 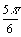) , E( 4 ; - ) .
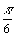b) Déterminer les coordonnées cartésiennes des points C, D, E .
c) Déterminer la mesure principale des angles orientés 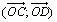et .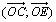
d) En déduire la nature des triangles ODC et OCE.
e) On pose 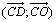= a ; montrer que 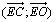= a .
f) En déduire la nature du triangle CDE. g) Calculer les longueurs CD, CE et DE et retrouver le résultat de la question précédente.

EXERCICE 5: Sur la figure ci-contre, le triangle ABC est rectangle et isocèle en A et les triangles ACD et ABE sont équilatéraux ( extérieur à ABC ) .
a) Déterminer la mesure des angles géométriques ^DAE , ^DEB et ^CBE .
b) En déduire une mesure, en radians, des angles orientés 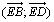et .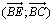
c) En utilisant la relation de Chasles, déterminer une mesure, en radians, de l'angle orienté .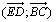
d) Que peut-on en déduire pour les droites (ED) et (BC) ?

Haut de page