a) Une construction due à Euclide (troisième siècle avant J.C.) : On considère le triangle AOF rectangle et isocèle en O; G est le milieu de [AO]; le cercle de centre G et passant par F coupe la demi droite [AO) en C. Soient B et H les points d'intersection des cercles C1 et C2 de rayon OA et de centres respectifs A et C avec B dans le même demi-plan que F par rapport à (OA). Soient D et E les intersections respectives de la droite (AH) avec C2 et de la droite (CH) avec C1.

b) On considère un cercle de centre O et de rayon OA. La droite perpendiculaire (OA) en O coupe le cercle en A'; le point B est le milieu de [OA']; le cercle de centre B et de rayon BA coupe (OA') en C à l'intérieur du cercle. Le cercle de centre A et de rayon AC coupe le cercle initial en A1 et A4 ; le côté du pentagone est AA1. Il n'y a plus qu'à reporter cette distance.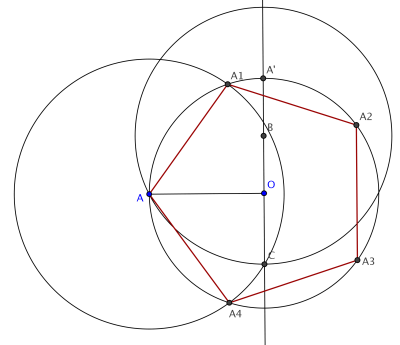

c) Une construction due à Richmond:

c) Une construction due à Richmond (1893): On considère un cercle de centre O, de rayon OA; la perpendiculaire à (OA) en O coupe le cercle en B; le point D est le milieu de [OB]. La bissectrice de l'angle coupe [OA] en E. La perpendiculaire à (OA) en E coupe le cercle en A1 et A4 . Le côté du pentagone régulier est AA1. Il ne reste plus qu'à reporter cette distance.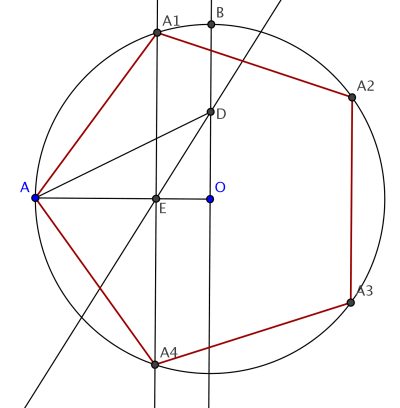