| Retour page seconde |
exercices seconde |
géométrie
EXERCICE 1:
Dans un triangle ABC, les points I, J et
K sont les milieux respectifs des côtés [AB], [BC] et [AC];
le point O est le centre du cercle circonscrit à ABC.
Montrer que le point O est l'orthocentre du triangle IJK.
EXERCICE 2
: Soit ABC un triangle équilatéral
de côté a; H est le milieu de [BC], D est le symétrique de B par rapport
à C et I est le milieu de [AD].
1. Faire une figure.
2. Calculer les distances AH, DH puis AD en fonction de a.
3. Montrer que le triangle ABD est rectangle en A.
4. Calculer la distance AI en fonction de a.
EXERCICE 3
: Soit ABCD un rectangle; soient I
le milieu de [BC], F le symétrique de A par rapport à D,
E le symétrique de A par rapport à I et H le point d'intersection des droites (IF) et
(CD).
a) Faire une figure.
b) Montrer que le point C est le milieu du segment [DE].
c) Montrer que H est le centre de gravité du triangle AEF.
d) Si AB=8 et AD=5, calculer AE, DH et AH.
EXERCICE 4 : ABCD
est un carré de côté 4 cm, de centre O; le point E est tel que le triangle ACE
est rectangle en C et CE=4 cm.
a) Calculer la longueur AC.
b) Calculer la longueur AE.
c) I est le point d'intersection des droites (AE) et (BD); montrer que I est le milieu du
segment [AE].
d) Calculer les distances IO et IC.
EXERCICE 5 : Dans le plan rapporté à un repère orthonormé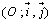 
(unité
graphique: 1 cm), on considère
les points A(0,-3), B(1,-1) et C(3,-2).
1. Déterminer, par le calcul, une équation cartésienne de la droite (AB).
2. Déterminer, par le calcul, une équation cartésienne de l'image de la droite
(AB)
par la translation de vecteur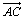 
.
3. a) Calculer les coordonnées des vecteurs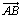 
et
.
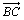b) Déterminer la nature du triangle ABC. Justifier les réponses.
EXERCICE 6 :
a) Dans le repère 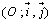orthonormé,
placer les points A( 3 ; 1), B( -1 ; -2), C( 4 ; -3) et D(-2 ;
5) .
b) Placer les points I, J, K et L milieux respectifs de [AC], [BC], [BD] et
[AD] et déterminer leurs coordonnées.
c) Calculer les longueurs AB et BD.
d) Les vecteurs et sont-ils colinéaires ?
e) Les vecteurs et sont-ils orthogonaux ?
f) Déterminer les coordonnées du centre de gravité G du triangle ABD.
g) Montrer que le quadrilatère IJKL est un rectangle ; déterminer les coordonnées
de son centre.