Ces exercices sont issues de devoir en classe ou à la maison donnés dans les années 2000, 2001, 2002; certains demandent de la réflexion. Le plus simple est de les imprimer et de travailler tranquillement sur papier. Les corrigés suivront...

EXERCICE 1: On considère deux points A et B et un point M quelconque en dehors de la droite (AB). a) Pour tout point G de [AB], montrer que G est le barycentre du système (A, aire(BMG)) et (B, aire(AMG)). b) La bissectrice de ^AMB coupe [AB] en G; montrer que G est le barycentre du système (A, MB) et (B , MA). c) Soit H la projection orthogonale de M sur (AB) ; on suppose que H appartient à [AB]. Montrer que H est le barycentre du système (A, tan(^MAB )) et (B, tan(^MBA)).

EXERCICE 2: On considère le triangle ABC. Soit P le barycentre du système de points pondérés {(A ;3),(B ;1),(C ;3)}.
a) Construire le point P.
b) Soit E le barycentre du système de points pondérés {(A ;3),(B ;1)}. Montrer que P est sur la droite (CE).
c) Montrer que (BP) coupe [AC] en son milieu J.
d) Soit G le centre de gravité du triangle ABC. Déterminer le réel k tel que .
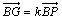e) Soit D le barycentre du système de points pondérés {(A ;1),(B ; -1),(C ;1)}. Construire le point D.
f) Trouver trois réels a, d, c tels que G soit le barycentre du système de points pondérés {(A ;a),(D ;d),(C ;c)}.

EXERCICE 3: On considère le triangle ABC rectangle et isocèle en B. Soit G le barycentre du système de points pondérés {(A ;1),(B ;2),(C ;3)}.
a) Construire le point G.
b) Soit E le barycentre du système de points pondérés {(A ;1),(B ;2)}. Montrer que G est le milieu de [EC].
c) Soit F le symétrique de C par rapport à B. Montrer que E est l'isobarycentre du triangle ACF.
d) Soit D l'image de A par la translation de vecteur 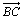. Déterminer le point H barycentre du système de points pondérés {(E ;3),(C ;3),(D ;6)}.
e) Trouver trois réels a, b, c tels que D soit le barycentre du système de points pondérés {(A ;a),(B ;b),(C ;c)}. Corrigé

Voir aussi les animations sur les barycentres

Haut de page