Ces exercices font partie de devoirs donnés
en classe durant l'année 2002 - 2003 ; ils sont tous corrigés,
ces corrigés sont au format PDF:
Exo 1 : (Etude
des courbes de deux fonctions exponentielles ; propriétés géométriques
) 1. a) Tracer dans un même repère orthonormé
les courbes C et C’ d’équations respectives y = ex
et y = e-x.
b) Soit a un réel quelconque ; T et T’ sont les tangentes
en a à, respectivement C et C’.
Montrer que T et T’ sont perpendiculaires (Propriété P1).
c) On note H le point de coordonnées (a ; 0) et B et B’
les points d’intersection de T et T’ avec l’axe des abscisses.
Montrer que H est le milieu de [BB’] (Propriété P2). Représenter
T, T’, B, B’ et H pour a = 2.
2. Généralisation : On considère une fonction
f dérivable sur IR, et les courbes C et C’ d’équation
y = f(x) et y = f(-x).
a) Montrer que la fonction f vérifie la propriété
P1 si f'(a)f'(-a) = 1 pour tout a tel que f ‘(a)
différent de 0.
b) Montrer que la fonction f vérifie la propriété
P2 si f(a)f'(-a) = f(-a)f'(a) pour tout a tel que f‘(a)
différent de 0.
c) Montrer que cette dernière propriété est équivalente
à f(a)f(-a) = k pour tout a tel que f'(a)
différent de 0 et où k est une constante réelle.
d) Trouver une condition sur les réels a et b pour
que les fonctions f de la forme f(x) = aexp(bx) possèdent
les propriétés P1 et P2.
e) Déterminer les réels a, b et c pour que les
fonctions f de la forme f(x) = aexp(bx + c) possèdent
les propriétés P1 et P2.
Corrigé
Exo 2 :
(Etude d'une fonction exponentielle, tangente à la courbe, position de
cette tangente ) On considère la fonction f définie
sur IR par 
et
Cf sa représentation graphique dans un repère 
.
a) Déterminer les limites de f en +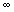
et en - .
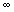Préciser les asymptotes à Cf .
b) Montrer que le point K(0 ; 0,5) est un centre de symétrie de Cf
.
c) Etudier les variations de f .
d) Déterminer une équation de la tangente à Cf
au point K.
e) Justifier que, pour étudier la position de la tangente T par rapport
à la courbe Cf , il suffit d’étudier sur IR le
signe de g(x) où g(x) = 2ex - xex
- 2 - x.
f) Calculer g’(x) et g’’(x) . Déterminer,
en les justifiant les signes de g’’(x), g’(x) et g(x)
. En déduire la position de T et de Cf .
g) Pour tout réel a strictement compris entre 0 et 1, résoudre
l’équation f(x) = a . Ecrire le plus simplement possible
la solution de l’équation f(x) = 1/3.
Corrigé
Exo 3 : (
Fonctions exponentielles, suites, primitive ) Partie A : On considère
la fonction f définie sur IR par f(x) = ex²
+ ax + b où a et b sont des réels.
a) Déterminer les valeurs de a et b pour lesquelles
le tableau de variations ci-contre est celui de la fonction f . Justifier
la réponse.
| x |
- |
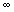1,5 |
+ |
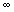| f'(x) |
- |
0 |
+ |
| f(x) |
+ |
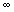e-1,25 |
+ |
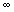b) Montrer que la droite d’équation y = 1,5 est un axe
de symétrie de la courbe représentative de la fonction f
.
Partie B : On considère la fonction g définie
sur IR par g(x) = (x² + 3x + 1)e-x.
a) Déterminer les limites de la fonction g aux bornes de son
ensemble de définition.
b) Etudier les variations de la fonction g . Dresser son tableau de
variations.
c) Tracer la courbe représentative de g dans un repère
orthonormé.
d) On considère la suite (un)définie par :
pour tout entier naturel n , 
. Interpréter graphiquement un et dessiner u3
sur le graphique de la question précédente.
e) Calculer le premier terme u0. Montrer que la suite (un)
est croissante.
f) Montrer que la fonction G définie sur IR par G(x) = (-x²
- 5x - 6)e-x est une primitive de g . Déterminer
alors un en fonction de n , puis calculer 
. Quelle est l’interprétation graphique de ce dernier résultat
?
Partie C : On considère la fonction h définie
sur IR par h(x) = e2x + cex + d où c et d
sont des réels.
a) Déterminer les valeurs de c et d pour que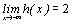 
et h'(ln1,5) = 0. Justifier la réponse.
b) Résoudre l’équation h(x) = 0.
Corrigé
Exo 4 : (Etude
d'une fonction exponentielle, dérivées successives, étude
de suites) La fonction f est définie sur IR par
. On note f', f'',f(3) , f(4)
, ... les dérivées successives de f.
1. Déterminer f'' et f(3).
2. Démontrer par récurrence que pour tout entier n supérieur
ou égal à 1, f(n)(x) = 2n(1 - n
- 2x)e2x.
3. Pour tout entier n non nul, la courbe représentative de f(n)
admet une tangente horizontale en un point noté Mn.
a) Calculer les coordonnées x et y de Mn et vérifier
que les points appartiennent à la courbe C d’équation 
.
b) Démontrer que la suite (xn) est une suite arithmétique.
Quelle est la limite de cette suite ?
c) Démontrer que la suite (yn) est une suite géométrique.
Etudier la limite de cette suite ?
Corrigé
Exo 5 : (Etude
d'une fonction exponentielle, dérivées successives, étude
de suites) La fonction f est définie sur IR par
f(x) = (x2 + x - 1)ex . On note f',
f'' = f(2), f(3) les dérivées
successives de f.
1. Calculer pour tout réel x, f ‘ et f''
.
2. a) Démontrer par récurrence que pour tout entier naturel n
supérieur ou égal à 1, f(n) (x) = (x2
+ anx + bn)e avec an+1 = an
+ 2 et bn+1 = an + bn .
b) Déduisez-en que an et bn
sont des entiers relatifs.
3. On se propose dans cette question d’exprimer an
et bn en fonction de n .
a) Vérifier que la suite an est une suite arithmétique.
Déduisez-en an en fonction de n pour tout
n supérieur ou égal à 1.
b) Vérifier que pour tout n supérieur ou égal
à 1 : bn = an-1 + an-2 + ... + a2
+ a1 . Déduisez-en bn en fonction
de n pour tout n supérieur ou égal à
1.
Corrigé
Exo 6 : PARTIE A :
On considère l’équation différentielle (E1) définie
par y' - 2y = 3ex - 4x + 2.
a) Résoudre l’équation différentielle (E2) définie
par y' - 2y = 0.
b) Montrer que la fonction u définie sur IR par u(x) = -3ex
+ 2x est solution de (E1).
c) Montrer qu’une fonction v est solution de (E2) si et seulement
si u + v est solution de (E1).
d) En déduire toutes les solutions de (E1).
e) Déterminer la solution f de (E1) telle que la courbe représentative
de f admette une tangente horizontale au point d’abscisse 0.
PARTIE B : On considère la fonction g définie
sur IR par g(x) = 0,5e2x - 3ex + 2x et Cg
sa courbe représentative dans un repère orthonormé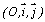 
.
a) Déterminer les limites de f en +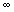
et en -.
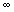b) Montrer que la droite (d) d’équation y = 2x
est asymptote à la courbe Cg . Préciser la position
relative de (d) et Cg .
c) Etudier les variations de la fonction g . Dresser son tableau de
variations.
d) Calculer l’aire comprise entre Cg , (d) et les droites d’équation
x = 0 et x = ln2.
Corrigé
Haut de page