Ces exercices font partie de devoirs donnés en classe durant l'année 2002 - 2003 ; ils sont tous corrigés, ces corrigés sont au format PDF :

Exo 1 : Soit le repère orthonormal direct (O ; i , j , k) dans l’espace. On considère les points A(2 ;-1 ;0), B(0 ;3 ;-4), D(4 ;1 ;1) et S(-2 ;1 ;4).
a) Montrer que les points A,B et D ne sont pas alignés.
b) Déterminer les coordonnées du point C pour que ABCD soit un parallélogramme.
c) Calculer le produit scalaire des vecteurs AB et AD. Que peut-on en déduire pour le quadrilatère ABCD ?
d) Calculer le produit scalaire des vecteurs AB et AS. En déduire une équation du plan (ABD).
e) La droite (d) passe par D et est parallèle à (AS). Déterminer une représentation paramétrique de (d).
f) Montrer que le vecteur u ( 1 ; -1 ; 0 ) est un vecteur normal au plan (SBC). La droite (d) coupe le plan (SBC) en E. Déterminer les coordonnées du point E.
Corrigé

Exo 2 : Soit le repère orthonormal direct (O ; i , j , k ) dans l’espace ( unité graphique : 1 cm).
On considère les points A(0 ; 6 ; 0), B(0 ; 0 ; 8), C(4 ; 0 ; 8).
1. a) Démontrer que les droites (BC) et (BA) sont orthogonales.
b) Démontrer que les droites (OC) et (OA) sont orthogonales.
c) Démontrer que la droite (BC) est orthogonale au plan (OAB).
d) Déterminer le volume, en centimètre cube, du tétraèdre OABC .
e) Démontrer que les quatre points O, A, B et C se trouve sur une sphère dont on déterminera le centre et le rayon.
2. A tout réel k de l’intervalle ouvert ]0 ; 8[, est associé le point M(0 ; 0 ; k). Le plan (G) qui contient le point M et qui est orthogonal à la droite (OB), rencontre les droites (OC), (AC), (AB) respectivement en N, P, Q.
a) Déterminer la nature du quadrilatère MNPQ.
b) La droite (PM) est-elle orthogonale à la droite (OB) ?
c) Pour quelle valeur de k, la droite (PM) est-elle orthogonale à la droite (AC) ?
d) Déterminer MP² en fonction de k . Pour quelle valeur de k, la distance PM est-elle minimale ?
Corrigé

Exo 3 : Dans le plan, on considère le triangle ABC isocèle en A, de hauteur [AH] tel que AH = BC = 4.
1. En justifiant la construction, placer le point G barycentre du système de points pondérés {(A, 2) ; (B, 1) ; (C ; 1)}.
2. On désigne par M un point quelconque du plan.
a) Montrer que le vecteur V = 2MA - MB - MC est un vecteur de norme 8.
b) Déterminer et construire l’ensemble E₁ des points M du plan tels que || 2MA + MB + MC || = || V ||.
3. On considère le système de points pondérés {(A, 2) ; (B, n) ; (C ; n)} où n est un entier naturel.
a) Montrer que, pour tout n, le barycentre G_n de ce système de points existe. Placer G₀, G₁, G₂.
b) Montrer que le point G_n appartient au segment [AH].
c) Calculer la distance AG_n en fonction de n et déterminer la limite de AG_n lorsque n tend vers +.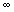
d) Soit l’ensemble (E_n) des points M du plan tels que || 2MA + nMB + nMC || = n|| V ||. Montrer que (E_n) est un cercle qui passe par le point A. Préciser le centre et le rayon de ce cercle.
e) Construire (E₂).
Corrigé

D'autres exercies au format PDF : exos geom

Haut de page