Ces exercices font partie de devoirs donnés en
classe durant l'année 2002 - 2003 ; ils sont tous corrigés, ces
corrigés sont au format PDF :
Exo 1 : (Transformation
du plan, étude de fonction, étude d'une suite, variations, convergence)
ABCD est un carré de côté 1 et I est le barycentre du système
de points pondérés {(A,1) ;(D,3)}. M est un point de la droite
(AB). Lorsque les droites (BI) et (CM) sont sécantes, on note P leur
point d’intersection, et H le projeté orthogonal de P sur la droite
(AD) ; le point M’ est le point d’intersection de (AB) avec la parallèle
à (BD) passant par H.
A. Etude de la transformation qui à M associe M’ :
1) Montrer qu’il existe un unique point M de (AB) pour lequel M’
n’est pas défini ; on note R ce point.
2) On désigne respectivement par t et t’ les abscisses des points
M et M’ dans le repère (A,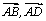 ).
).
a) Démontrer que 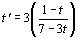 .
.
b) Déterminer les points M de (AB) tels que M = M’. ( On appellera
E celui qui appartient à [AB] et F l’autre).
c) Déterminer les points M de (AB) tels que M’ appartient à
[AM].
3) a) Etudier les variations de la fonction f définie sur IR
\ {7/3} par f(t) = 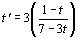 et
calculer ses limites aux bornes de son ensemble de définition.
et
calculer ses limites aux bornes de son ensemble de définition.
b) Tracer la courbe représentative de f dans un repère
orthonormal 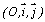 (unité
5 cm), en précisant ses asymptotes et ses éléments de symétrie.
(unité
5 cm), en précisant ses asymptotes et ses éléments de symétrie.
c) Résoudre graphiquement les inéquations 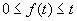 et
retrouver le résultat de la question 2)c).
et
retrouver le résultat de la question 2)c).
d) Démontrer que si M appartient à [AB] alors M’ appartient
à [AB].
B. Etude d’une suite :
On s’intéresse à la suite de points (An)
du segment [AB] définie par : A0= A et pour tout
entier naturel n , An+1 est le point M’ obtenu
à partir du point M = An. On désigne par tn
l’abscisse du point dans le repère (A,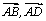 ). Ainsi, pour tout entier naturel n , on a
). Ainsi, pour tout entier naturel n , on a 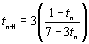 .
.
1)a) En utilisant le droite d’équation y = x et la courbe
Cf, représenter sur l’axe des abscisses les
cinq premiers termes de la suite (tn).
b) La suite est-elle monotone ? Justifier la réponse. Faire une conjecture
sur la convergence de cette suite.
2) a) Démontrer que la suite (un)définie par
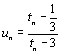 est
une suite géométrique dont on précisera le premier terme
et la raison.
est
une suite géométrique dont on précisera le premier terme
et la raison.
b) Exprimer un, puis tn en fonction
de n .
c) La suite (tn)converge-t-elle ? Si oui, donner sa limite.
Interpréter ce résultat géométriquement.
Corrigé
Exo 2 : (
Etude des variations et de la convergence d'une suite, suite auxiliaire, suite
géométrique )
On considère la suite (un) numérique définie
par u0 = 1/2 et 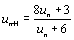 .
.
a) Démontrer par récurrence que, pour tout entier n supérieur
ou égal à 1, on a 1 < un < 3 .
b) Montrer que la suite (un) est croissante. La suite converge-t-elle
?
c) On considère la suite numérique (vn) définie
pour tout entier naturel n par 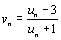 . Démontrer que la suite (vn) est géométrique
et préciser sa raison et son premier terme.
. Démontrer que la suite (vn) est géométrique
et préciser sa raison et son premier terme.
e) Quelle est la limite de la suite (vn) ?
f) Exprimer, pour tout entier naturel n , un en
fonction de n .
g) En déduire le comportement de (un) lorsque n
tend vers l’infini.
Corrigé
Exo 3 : (
Etude des variations et de la convergence de deux suites, suite auxiliaire,
suites adjacentes )
On considère deux réels a et b tels que 0 <
a < b, et les deux suites (un) et (vn)
définies par u0 = a, v0
= b, 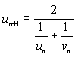 et
et
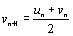 ;
;
(rappel : un+1 est la moyenne harmonique de un
et vn; vn+1 est la moyenne arithmétique
de un et vn ) .
Le but du problème est de montrer que les deux suites sont adjacentes,
de trouver leur limite commune et d’en déduire des approximations
de réels par des rationnels.
a) Montrer que, pour tout entier naturel n, un
et vn sont strictement positifs.
b) Montrer que, pour tout entier naturel n, un
< vn .
c) Montrer que, pour tous réels x et y tels que 0 <
x < y , on a 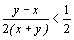 .
En déduire que
.
En déduire que 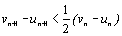 .
.
e) Montrer par récurrence que, pour tout entier naturel n >
0, on a 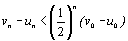 .
.
f) En déduire la limite de vn - un
.
g) Montrer que les suites (un) et (vn)
sont adjacentes.
h) Montrer que, pour tout entier naturel n, le produit unvn
est constant. En déduire la limite des suites (un)
et (vn) .
i) Donner alors un encadrement de 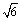 par
deux rationnels au cent millième près.
par
deux rationnels au cent millième près.
Corrigé
Exo 4 : (
Etude des variations et de la convergence de deux suites, suites auxiliaires,
suites adjacentes )
On considère les deux suites (un) et (vn)
définies par u0 = 0 , 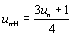 et
v0 = 2,
et
v0 = 2, 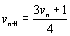 ;
;
a) On considère la suite (sn) définie par
sn = un + vn .
Montrer par récurrence que la suite est constante .
b) On considère la suite (dn) définie par
dn = vn - un. Montrer
que la suite est une suite géométrique dont on donnera la raison
et le premier terme.
c) En déduire 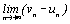 .
.
d) Ecrire  en
fonction de sn et de dn , puis en fonction
de n . Ecrire vn en fonction de sn
et de dn , puis en fonction de n . En déduire
la limite de un et celle de vn .
en
fonction de sn et de dn , puis en fonction
de n . Ecrire vn en fonction de sn
et de dn , puis en fonction de n . En déduire
la limite de un et celle de vn .
e) Les suites (un) et (vn) sont-elles
adjacentes ?
Corrigé
Exo 5 : (Etude
d'une suite d'intégrales, étude de fonction, convergence de suite
) On considère la suite (un) définie
sur IR par 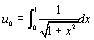 et
pour n supérieur ou égal à 1,
et
pour n supérieur ou égal à 1, 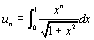 .
.
a) Soit f la fonction définie sur [0 ; 1] par 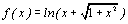 .
Calculer f ‘ (x) et en déduire u0.
.
Calculer f ‘ (x) et en déduire u0.
b) Calculer u1.
c) Pour tout entier n supérieur ou égal à 1 et
pour tout x de [0 ; 1], comparer xn et xn+1
. En déduire que la suite (un) est décroissante.
d) Démontrer que, pour tout x de [0 ; 1], 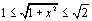 .
.
e) En déduire que, pour tout entier n supérieur ou égal
à 1, 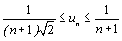 .
.
f) En déduire que (un) converge et déterminer
sa limite.
Corrigé
Exo 6 : (Etude
d'une suite d'intégrales, étude de fonction, calcul des premiers
termes de la suite ) On considère la fonction f
définie sur ]0 ; +  [
par
[
par 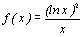 .
.
1. Déterminer les limites de f en 0 et en + .
.
2. Calculer la dérivée de f et déterminer son
sens de variations sur ]0 ; +  [.
[.
3. Tracer la représentation graphique de f dans le plan.
4. On pose, pour p supérieur ou égal à 1, 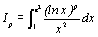 .
A l’aide d’une intégration par parties, calculer la valeur
exacte de I1 .
.
A l’aide d’une intégration par parties, calculer la valeur
exacte de I1 .
5. Montrer que, pour p supérieur ou égal à 1,
. En déduire les valeurs exactes de I2 , I3
, I4 .
Corrigé
Exo 7 : Pour n entier
naturel non nul, soit la fonction fn définie sur
I = [0 ; + 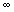 [
par
[
par 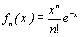 .
On considère un réel a de I et on pose, pour tout entier
naturel n,
.
On considère un réel a de I et on pose, pour tout entier
naturel n, 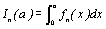 .
.
1. Calculer I0(a).
2. a) Montrer que, pour tout x de I et pour tout n entier
naturel non nul : fn'(x) = fn-1(x) - fn(x)
et fn(0) = 0.
b) En déduire que, pour tout n entier naturel non nul : In(a)
- In-1(a) = 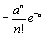 .
.
c) En déduire que, pour tout n entier naturel non nul : In(a)
= 1 - 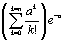 .
.
3. Dans cette question, on pose a = 1. On appelle (un)
la suite numérique définie pour tout entier naturel n
par : 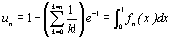 .
.
a) Montrer que, pour tout entier naturel n, et pour tout x
de [0 ;1] : 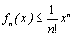 .
.
b) En déduire l’encadrement pour tout entier naturel n
: 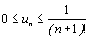 puis la limite de (un) .
puis la limite de (un) .
c) Déduire enfin que 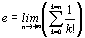 =
1 +
=
1 + 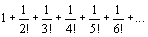
Corrigé
Haut de page
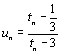 est
une suite géométrique dont on précisera le premier terme
et la raison.
est
une suite géométrique dont on précisera le premier terme
et la raison. 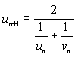 et
et