Ces exercices font partie de devoirs donnés en classe durant l'année 2002 - 2003 ; ils sont tous corrigés, ces corrigés sont au format PDF :

Exo 1 : On considère le polynôme P défini par P(x) = .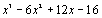
a) Calculer P(4). En déduire une factorisation de P.
b) Déterminer les solutions de l’équation P(x) = 0 dans .
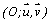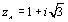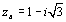c) On considère le repère orthonormé du plan et les points A, B, C d’affixes respectives , et .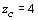
d) Déterminer le module et un argument de z_A et z_B. Placer les trois points A, B et C dans le plan.
e) Déterminer la nature du triangle ABC.
Corrigé

Exo 2 : 1. On considère l’équation (E) dans l’ensemble des nombres complexes définie par : z² - 6z + 12 = 0 .
a) Résoudre l’équation (E) ; on note u et v ses solutions, u étant celle dont la partie imaginaire est positive.
b) Calculer le module et un argument de u ; en déduire le module et un argument de v.
2. a) On considère le nombre complexe u - 4 ; écrire ce nombre complexe sous forme algébrique, puis sous forme trigonométrique.
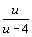b) Calculer le module et un argument du nombre complexe ; en déduire le module et un argument du nombre complexe .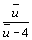
3. Dans le plan complexe rapporté à un repère orthonormé 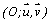, on note A le point d’affixe 4, B le point d’affixe 2 et C le point d’affixe 6 ; M et N sont les points d’affixes u et v.
a) Démontrer que les points O, A, M et N sont sur un même cercle que l’on précisera.
b) Démontrer que les points B, C, M et N sont aussi sur un même cercle que l’on précisera.
c) Construire les deux cercles ainsi obtenus et les points M et N.
Corrigé

Exo 3 : Dans le plan complexe rapporté à un repère orthonormé 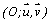(d’unité graphique 2 cm) , on considère le point A₀ d’affixe 2, le point A'₀ d’affixe 2i et le point A₁ milieu du segment [A₀A'₀]. Plus généralement, si A_n est un point d’affixe z_n, on désigne par A'_n le point d’affixe i z_n , et par A_n+1 le milieu de [A_nA'_n ]. On note r_n et T_n le module et un argument de z_n .
1. a) Déterminer les affixes des points A₁, A'₁, A₂, A'₂, A₃. Placer ces points sur une figure.
b) Calculer r₀, r₁, r₂, r₃ et T₀ , T₁, T₂, T₃.
2. a) Pour tout entier n , exprimer z_n+1 en fonction de z_n ; en déduire z_n en fonction de n .
b) Etablir les expressions de r_n et T_n en fonction de n .
c) Déterminer la limite de r_n quand n tend vers l’infini. Interpréter géométriquement ce résultat.
d) Comparer les modules et les arguments de z_n et z_n+8.
3. Etablir que 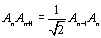. Après avoir exprimer A_nA_n+1 en fonction de n , déterminer, en fonction de n , la longueur l_n de la ligne brisée A₀A₁A₂...A_n. Déterminer la limite de l_n lorsque n tend vers l’infini.
Corrigé

Exo 4 : a) On considère le nombre complexe m = 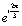; écrire m et m² sous forme algébrique.
b) Montrer que 1 + m + m² = 0 et n = m², où n désigne le conjugué de m.
c) Montrer que |m|= |1 + m| ; le complexe n vérifie-t-il la même égalité ?
d) On considère un nombre complexe z vérifiant la relation | z | = |1 + z |;
montrer que la partie réelle de z vérifie Re(z) = -0,5 .
e) On considère un nombre complexe z différent de -1 et de 0 vérifiant la relation Arg( z ) =Arg(1 + z ) ; montrer que z est réel.
Corrigé

Exo 5 : a) Résoudre dans l’ensemble des nombres complexes l’équation 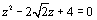. Ecrire les solutions sous la forme exponentielle complexe.
b) Dans le plan complexe, rapporté à un repère orthonorm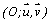é ( unité graphique : 2 cm), placer les points A, B et C d’affixe respective , , .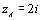
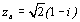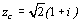c) Montrer que .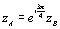
d) Déterminer l’affixe du point D vérifiant 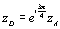. Placer le point D.
e) Montrer que z_B = iz_D.
f) Montrer que les quatre points A, B, C et D sont sur un même cercle dont on précisera le centre et le rayon.
Corrigé

Exo 6 : Pour x et y réels, on pose : z = x + iy , z^- = x - iy .
Déterminer les réels x et y tels que z z^- - 2z = 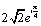; on note z₁ la solution de cette équation de partie réelle positive et z₂ l’autre. Déterminer les modules de z₁ et z₂.
Corrigé

Exo 7 : On considère un triangle ABC tel que l’angle (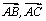 ) = a compris entre 0 et pi. On construit extérieurement au triangle ABC, les carrés ACRS et BAMN ainsi que le parallélogramme MASD. Montrer que les droites (AD) et (CB) sont perpendiculaires et que AD = BC.
Corrigé

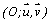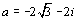Exo 8 : Le plan est rapporté à un repère orthonormal .On considère les points A et B d’affixes respectives et .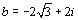
a) Calculer les distances OA, OB et AB. En déduire la nature du triangle OAB.
b) On désigne par C l’image de A par la rotation de centre O et d’angle pi/3. Déterminer l’affixe c du point C.
c) On désigne par D l’image de A par l’homothétie de centre O et de rapport 2. Déterminer l’affixe d du point D.
d) Placer les points A, B, C, D sur une figure (unité graphique : 1 cm).
e) Préciser la nature du triangle BCD en la justifiant.
f) Soit E le symétrique de D par rapport à I, milieu de [BC]. Montrer que le point E est l’image de C dans la rotation de centre B et d’angle pi/3.
Corrigé

Exo 9 : 1. On considère le polynôme P(z) = z⁴ + 8z³ + 24z² + 32z + 20 où z est un nombre complexe. Déterminer les nombres réels a et b tels que P(z) = (z² + az + b)(z² + 2z + 2). Résoudre dans l’équation P(z) = 0.
2. Le plan complexe est rapporté au repère orthonormé 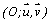(unité graphique : 2 cm) et on considère les points B, C, D, E d’affixes respectives b = -1 + i , c = -1- i , d = -3- i , e = -3 + i.
Montrer que le quadrilatère BCDE est un carré.
3. On considère le cercle K de centre O et passant par B. a) Déterminer une équation de K.
Soit Q un point de K distinct de B et C. L’affixe de Q est z = x + iy . Soient F et G les points du plan, d’affixes f et g, tels que QBFG soit un carré de sens direct, c’est-à-dire que 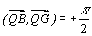. On pose .
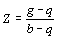b) Interpréter géométriquement le module et un argument de Z . En déduire Z.
c) Montrer que g = ( -1 + x+ y) + i( -1 - x + y). En déduire le module de g en fonction de x et de y .
d) En utilisant la question 3 a), exprimer le module de g en fonction de x .
e) Exprimer g + 1 + i en fonction de x et de y . En déduire le lieu de G lorsque Q décrit le cercle K.
f) A l’aide de considérations géométriques, montrer que | f | = | g |.
g) Pour quelles valeurs de x et de y les points D, E, F, G sont-ils sur un même cercle de centre O ? Préciser le rayon de ce cercle.
Corrigé

 D'autres exercices et problèmes au format PDF: exos complexes

Haut de page