Ces exercices sont issues de devoir en classe
ou à la maison donnés dans les années 2000, 2001, 2002;
certains demandent de la réflexion. Le plus simple est de les imprimer
et de travailler tranquillement sur papier. Les corrigés sont au format
PDF ; ils n'y sont pas tous, patience...
EXERCICE 1: On
considère la fonction f définie par f(x) =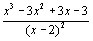 et (C) sa courbe représentative.
et (C) sa courbe représentative.
a) Préciser l’ensemble de définition de la fonction
f .
b) Déterminer les réels a, b, c, d tels que f(x)
=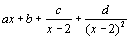 .
.
c) Soit (d) la droite d’équation y = x + 1 ;
en étudiant le signe de f(x) - (x + 1) , déterminer la position
de la courbe (C) par rapport à la droite (d).
d) Soit (d’) la droite d’équation y = 4x -
6 ; déterminer les abscisses des points d’intersection de (C)
et de (d’).
EXERCICE 2 : On
considère le carré ABCD de côté 1, et le carré BFEC. M est un point quelconque
de la demi-droite [BF), distinct de B. La droite (MC) coupe (AD) en N. On pose
AM = x et AN = y .
1. Montrer que y =x/(x-1) et montrer que MN² =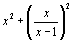 .
.
2. Le but de cette question est de montrer que MN2
est supérieure ou égale à 8 .
Première méthode : On pose g(x) = MN2
- 8.
a) Montrer que g(x) =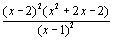 .
.
b) Etudier le signe de g(x). En déduire que, si
x > 1, alors g(x) est minimum pour x = 2.
c) Calculer MN² pour cette valeur, et préciser la position
de C sur le segment [MN].
Deuxième méthode : d) Montrer que si AM > 2, alors
AN < 2.
e) Montrer que l’aire du triangle AMN est
supérieur ou égale à 2 . En déduire que MN² est supérieur ou égale à
8 .
3. Montrer que C est le barycentre des points pondérés
(M, y) et (N, x).
4. Déterminer a et b, dépendants de x, tels que M est le
barycentre des points pondérés (A , a) et (B , b).
EXERCICE 3 : a)
On considère la fonction f définie sur IR par f(x) =
a x3 + bx² + cx + d et (C) sa courbe représentative. Cette courbe
passe par les points I(1 ;0), J(0 ;1), A(2 ;5) et B(- 1 ;
- 4) . Déterminer alors a, b, c, d.
b) Préciser, par lecture graphique les variations de f .
c) Déterminer les abscisses des points d’intersection de (C) et
l’axe (Ox).
d) Représenter graphiquement la fonction v définie par v(x)
= | f(x) | .
e) On s’intéresse à la partie de la courbe située sur
l’intervalle [0 ; 1].
On pose g la restriction de f à l’intervalle
[0 ; 1 ]. Représenter graphiquement chacune des fonctions h, k, l suivantes :
h(x) = - g(x) ; k(x) = g(- x ) ; l(x) = - g( - x)
.
EXERCICE 4 : On
considère la fonction f définie sur IR et les fonctions g ,
h , k définie par : g(x) = f(x - 5) - 2 ; h(x) = - f(x) et
k(x) = f(- x) . Préciser les transformations utilisées pour
passer de la courbe Cf à chacune des courbes Cg , Ch
, Ck .
EXERCICE 5 : On
considère les fonctions f et g définies par f(x) =3/(x-2)
et g(x) = x² + 2.
Déterminer la fonction fo g et go f . Préciser les
ensembles de définition de ces quatre fonctions.
EXERCICE 6 : Sur la branche de l’hyperbole d’équation y
= 1/x avec x > 0, on place les points M et N d’abscisses
respectives x et x + 1. Les points M et N se projettent orthogonalement
sur l’axe des abscisses en m et n ( d’un repère orthonormal).
Calculer l’aire de chacun des triangles OMm et ONn. Montrer
que le trapèze MNnm et le triangle OMN ont la même aire. Soit S la fonction
qui à x associe l’aire du triangle OMN. Déterminer les limites de
S en 0+ et en + infini . Corrigé
EXERCICE 7 : On
considère la fonction f définie par f(x) =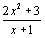 et Cf sa courbe représentative dans un repère (O;i ,j
) .
et Cf sa courbe représentative dans un repère (O;i ,j
) .
1. Préciser l’ensemble de définition Df
de la fonction f .
2. Déterminer les réels a, b et c
tels que f(x) =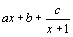 .
.
3. Déterminer les limites de f aux bornes de l’ensemble
Df . Préciser les asymptotes éventuelles à Cf
.
4. Montrer que la droite (d) d’équation y = 2x
- 2 est asymptote oblique à la courbe Cf .
5. On considère les points M et P d’abscisse x
, M sur Cf et P sur (d).
Déterminer le plus petit entier n tel que MP <
10-3 .
6. Résoudre l’équation f(x) = 5.
EXERCICE 8 : On
considère la fonction f définie par f(x) =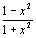 . Préciser l’ensemble de définition D de f .
. Préciser l’ensemble de définition D de f .
a) Etudier la parité de f .
b) Déterminer les limites de f aux bornes de son
ensemble de définition D.
Préciser les éventuelles asymptotes à la courbe (C) représentative
de f .
c) Montrer que f(x) =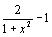 .
En déduire que pour tout x de D, -1 <= f(x) <= 1.
-1 est-il le minimum de f ? 1 est-il le maximum de f ?
.
En déduire que pour tout x de D, -1 <= f(x) <= 1.
-1 est-il le minimum de f ? 1 est-il le maximum de f ?
d) Déterminer la fonction dérivée de f . Déterminer
l’équation de la tangente à (C) au point d’abscisse 1 . Corrigé
EXERCICE 9 : On
considère la fonction h définie sur ]0 ; +infini [ par h(x) =1/x
, et (H) sa représentation graphique dans un repère (O;i ,j ). Soit M le
point de (H) d’abscisse a > 0.
a) Déterminer l’équation de la tangente (T) à (H)
en M.
b) Cette tangente coupe l’axe des abscisses en D et
l’axe des ordonnées en C. Déterminer les coordonnées de C et D.
c) Montrer que, pour tout a > 0, l’aire
du triangle OCD est égale à 4.
d) Déterminer l’équation de la normale (N) à (H) en
M.
e) Pour tout a différent de 1, F est le point d’intersection
de cette normale (N) et de la droite (d) d’équation y = x. Pour
a = 1, F a pour coordonnées (2 ; 2). Montrer que l’abscisse
de F est (a²+1)/a.
f) Montrer que, pour tout a > 0,le produit scalaire
DF.CF= 0 . Que peut-on en déduire ? Corrigé
EXERCICE 10 :
On considère la fonction f définie sur IR par f(x) =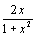 .
.
a) Etudier la parité de f . Que peut-on en déduire
pour la courbe (C) représentative de f ?
b) Déterminer les limites de f aux bornes de son
ensemble de définition. Préciser les éventuelles asymptotes.
c) Déterminer la dérivée de f . Dresser le tableau
de variations de la fonction f .
d) Montrer que (C) coupe la droite (d) d’équation
y = x en trois points. Préciser la position de (C) par rapport à (d).
e) On considère la fonction g définie sur IR par
g(x) =| f(x) |.
Exprimer la quantité 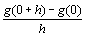 . La fonction g est-elle dérivable en 0 ? Corrigé
. La fonction g est-elle dérivable en 0 ? Corrigé
EXERCICE 11 :
ABCDEFGH est un cube d’arête 1 ; on considère le repère orthonormal
de l’espace (A ;AB ,AD ,AE ); soit I le milieu de [EH] et R
le point d’intersection des droites (EG) et (FI) ; soit J le milieu
de [CG] et S le point d’intersection des droites (CH) et (JD). Faire une
figure. Déterminer la distance RS. Soit M un point variable du segment [GH] ;
on pose HM = x . Exprimer la distance RM + MS en fonction de x.
Pour quelle valeur de x cette distance est-elle minimale ? Corrigé
EXERCICE 12 :
On considère sur ] -1 ; 1 ] les fonctions f, g, h définies par :
f(x) =1/(1+x) , g(x) = 1 - x , h(x) = 1 - x
+ x² . Représenter les trois courbes Cf Cg Ch
dans un même repère. Etudier le signe des différences f - g , h - f .
En déduire une comparaison des fonctions f, g, h sur ] -1 ; 1 ]
.
En déduire les 15 premières décimales de 1/(1 + 10-8) .
EXERCICE 13 :
Soit OAB un triangle rectangle en O et H le projeté orthogonal de O sur
(AB).
Montrer que 1/OH²= 1/OA²+1/OB² .
On considère le tétraèdre trirectangle OABC, c’est-à-dire
que les triangles OAB, OAC et OBC sont rectangles en O.
Démontrer que le point H projeté orthogonal de O sur le
plan (ABC) est l’orthocentre du triangle ABC.
En déduire que 1/OH²= 1/OA²+ 1/OB²+ 1/OC².On considère
maintenant que OA = OB = 1 et OC = x > 0. Déterminer la longueur OH
en fonction de x .
Montrer que pour tout x > 0, OH <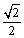 . Corrigé
. Corrigé
EXERCICE 14:
On considère la fonction f définie par f(x) = 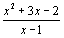 . Préciser l'ensemble de définition Df
de f .
. Préciser l'ensemble de définition Df
de f .
a) Vérifier que, pour tout x de Df , f(x) peut s'écrire
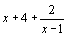 .
.
b) Déterminer la fonction dérivée de la fonction f et étudier son signe.
c) Déterminer les valeurs exactes des extremas locaux de la fonction f , sur
chacun des intervalles ] -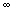 ; 1 [ et ] 1 ; +
; 1 [ et ] 1 ; +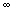 [ .
[ .
d) Dresser alors le tableau de variations de la fonction f .
e) Déterminer l'équation de la tangente à la courbe Cf , représentative de la
fonction f , au point d'abscisse 0.
f) On considère la droite (d) d'équation y = x + 4 ; étudier la position relative
de Cf et (d) .
g) Préciser les coordonnées des points d'intersection de Cf avec l'axe des abscisses.
EXERCICE
15 : On considère le rectangle ABCD tel que AB = 1 et AD = 2 ; I
est le milieu du segment [AB]. M est un point quelconque du segment [AD], et
on pose AM = x et f (x) = MI2 + MC2 .
a) Montrer que f (x) = 2 (x - 1)2 + 134 . En déduire le tableau de
variations de f .
b) Calculer IC2. Déterminer x pour que le triangle IMC soit rectangle
en M.
c) Expliquer alors la construction du ( ou des) point(s) M et faire une figure.
d) La médiatrice de [IC] coupe (AD) en K. Déterminer la longueur AK.
e) Déterminer x pour que MI > MC.
f) Déterminer les nombres dérivés de la fonction f pour x = 1 et x = 0. Corrigé
EXERCICE
16 : On considère la fonction f définie par f(x) = 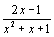 . Préciser
l'ensemble de définition Df de f .
. Préciser
l'ensemble de définition Df de f .
a) Déterminer la fonction dérivée de la fonction f et étudier son signe.
b) Déterminer les valeurs exactes des extremas de la fonction f sur IR .
c) Dresser alors le tableau de variations de la fonction f .
d) Déterminer l'équation de la tangente à la courbe Cf , représentative
de la fonction f , au point d'abscisse 0.
e) Déterminer le(s) antécédent(s) de -1 par f .
f) Préciser les coordonnées de(s) point(s) d'intersection de Cf avec
l'axe des abscisses.
EXERCICE
17 : Dans un repère orthonormé
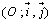 ,
on considère l'hyperbole H d'équation y = 1/x , et les points A(1 ; 1) et B(
-1 ; -1). On considère un point M de l'hyperbole H distinct de A et B, d'abscisse
m .
,
on considère l'hyperbole H d'équation y = 1/x , et les points A(1 ; 1) et B(
-1 ; -1). On considère un point M de l'hyperbole H distinct de A et B, d'abscisse
m .
a) Déterminer l'équation de la hauteur issue de A et l'équation de la hauteur
issue de M dans le triangle ABM. Soit K le point d'intersection de ces deux
hauteurs. Déterminer les coordonnées de K et montrer que K appartient à H.
b) Montrer que les coordonnées de W, centre du cercle C circonscrit au triangle
ABM, sont 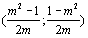 . c) Dans cette question, on prend m = 3. Déterminer l'équation du cercle C
. Question subsidiaire : En utilisant le changement de variable X = x + 1/x
, déterminer les coordonnées du quatrième point d'intersection de C et de H.
. c) Dans cette question, on prend m = 3. Déterminer l'équation du cercle C
. Question subsidiaire : En utilisant le changement de variable X = x + 1/x
, déterminer les coordonnées du quatrième point d'intersection de C et de H.
EXERCICE
18 : Cet exercice donne une généralisation d'une partie de l'exercice
précédent : Dans un repère orthonormé
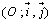 ,
on considère l'hyperbole H d'équation y = 1/x , et les points A, B et C distincts
appartenant à H , d'abscisses respectives a, b, c . Déterminer les coordonnées
de l'orthocentre K du triangle ABC, en fonction de a, b, c et vérifier qu'il
appartient à l'hyperbole H . Corrigé
,
on considère l'hyperbole H d'équation y = 1/x , et les points A, B et C distincts
appartenant à H , d'abscisses respectives a, b, c . Déterminer les coordonnées
de l'orthocentre K du triangle ABC, en fonction de a, b, c et vérifier qu'il
appartient à l'hyperbole H . Corrigé
EXERCICE
19 : On considère la fonction h définie sur IR \ {1} par h(x) = 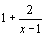 et H sa représentation graphique dans un repère orthonormé
et H sa représentation graphique dans un repère orthonormé  .
.
a) Etudier les limites de h aux bornes de son ensemble de définition. Préciser
les équations des asymptotes à H.
b) Etudier les variations de h et dresser son tableau de variations.
c) Déterminer une équation de la tangente (T) à H au point A d'abscisse 2.
d) On considère la fonction f définie sur IR par f(x) = ax² + bx -1 où a et
b sont des réels. On appelle P sa représentation graphique dans le repère orthonormé
 .
Déterminer les réels a et b pour que H et P aient la même tangente en A.
.
Déterminer les réels a et b pour que H et P aient la même tangente en A.
e) Déterminer alors les limites de f en + 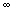 et
en -
et
en - 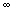 .
.
f) Dresser le tableau de variations de f . g) Représenter (T), H et P dans le
même repère. Résoudre graphiquement l'inéquation f(x) < h(x). Corrigé
EXERCICE
20: On considère la fonction f définie sur IR\{1} par f(x) = 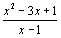 . a) Vérifier que f(x) =
. a) Vérifier que f(x) = 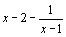 .
.
b) Déterminer les limites de la fonction f aux bornes de son ensemble de définition.
Préciser les éventuelles asymptotes à la courbe Cf représentative de la fonction
f .
c) Montrer que la droite (d) d'équation y = x - 2 est asymptote oblique
à la courbe Cf .
d) Déterminer la dérivée de f et étudier les variations de
f . Dresser le tableau de variations de f .
e) Déterminer la position relative
de la courbe Cf et de la droite (d).
f) Préciser les abscisses des points d'intersection
de la courbe Cf avec l'axe des abscisses.
g) Y a-t-il une ou des tangentes à
la courbe Cf parallèle à la droite (d) ? Si oui, préciser en quels points .
h) Déterminer les coordonnées du point d'intersection des tangentes à Cf aux
points d'abscisses 1/2 et 2 .
i) Représenter, dans un repère orthonormé 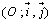 ,
la courbe Cf , les asymptotes et les tangentes des questions précédentes . Corrigé
,
la courbe Cf , les asymptotes et les tangentes des questions précédentes . Corrigé
EXERCICE
21 : On considère la fonction g définie sur [0 ; 2] par g(x) = 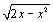 et Cg sa courbe représentative dans un repère orthonormé
et Cg sa courbe représentative dans un repère orthonormé 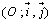 .
a) En posant y = g(x) et en calculant y² , montrer que la courbe Cg est un demi-cercle
dont on précisera le centre et le rayon.
.
a) En posant y = g(x) et en calculant y² , montrer que la courbe Cg est un demi-cercle
dont on précisera le centre et le rayon.
b) Calculer 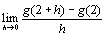 . En déduire si la fonction g est dérivable en 2.
. En déduire si la fonction g est dérivable en 2.
c) Déterminer la dérivée de g et dresser son tableau de variations .
d) On considère la fonction h définie sur IR par h(x) = 13 x3 - 2x2
+ 3x - 13 et Ch sa représentation graphique dans le repère 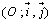 .
Déterminer les limites de h en +
.
Déterminer les limites de h en +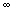 et
en -
et
en -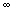 .
.
e) Etudier les variations de h . Dresser son tableau de variations.
f) Préciser le point où Ch et Cg ont une tangente (T) commune.
g) Représenter, dans le repère 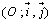 ,
les courbes Ch et Cg ainsi que la tangente (T). Corrigé
,
les courbes Ch et Cg ainsi que la tangente (T). Corrigé
Haut de page